15-112
Fall-17

Home

Syllabus

Schedule

Gallery

Staff

Piazza

Autolab

OH Queue

CMU 15-112 Fall 2017: Fundamentals of Programming and Computer Science
Homework 7 (Due Saturday, 14-Oct, at 8pm)

  1. Take an Old Midterm [15 pts] [manually graded]
    In order to help you start studying for the exam, the first part of this homework is to take an old midterm.

    Print out a copy of the Fall 2016 Midterm #1. Set a timer for 80 minutes and take the midterm in that time. (Treat this as if you are taking a real exam.) When you are done, scan a copy of your midterm as a PDF and submit it on autolab to "hw7-midterm". If you don't have an easy way to scan to PDF, consider the phone app CamScanner or Tiny Scanner (iOS|Android).

    This activity will not be graded for correctness, but instead simply to verify that you did it.

    Note: Grace days may not be used for the midterm PDF submission. (But can be used for the code below.) So, do this first.
  2. invertDictionary(d) [30 pts] [autograded]
    Write the function invertDictionary(d) that takes a dictionary d that maps keys to values and returns a dictionary of its inverse, that maps the original values back to their keys. One complication: there can be duplicate values in the original dictionary. That is, there can be keys k1 and k2 such that (d[k1] == v) and (d[k2] == v) for the same value v. For this reason, we will in fact map values back to the set of keys that originally mapped to them. So, for example: 
    assert(invertDictionary({1:2, 2:3, 3:4, 5:3}) == 
       {2:set([1]), 3:set([2,5]), 4:set([3])})
    Also, you may assume that the values in the original dictionary are all immutable, so that they are legal keys in the resulting inverted dictionary.

  3. friendsOfFriends(d) [35 pts] [autograded]
    Background: we can create a dictionary mapping people to sets of their friends. For example, we might say: 
        d["jon"] = set(["arya", "tyrion"])
    d["tyrion"] = set(["jon", "jaime", "pod"])
    d["arya"] = set(["jon"])
    d["jaime"] = set(["tyrion", "brienne"])
    d["brienne"] = set(["jaime", "pod"])
    d["pod"] = set(["tyrion", "brienne", "jaime"])
    d["ramsay"] = set()
    With this in mind, write the function friendsOfFriends(d) that takes such a dictionary mapping people to sets of friends and returns a new dictionary mapping all the same people to sets of their friends of friends. For example, since Tyrion is a friend of Pod, and Jon is a friend of Tyrion, Jon is a friend-of-friend of Pod. This set should exclude any direct friends, so Jaime does not count as a friend-of-friend of Pod (since he is simply a friend of Pod) despite also being a friend of Tyrion's. Also, do not include anyone either in their own set of friends or their own set of friends-of-friends.
    Thus, in this example... if fof = friendsOfFriends(d), then fof looks like: 
    {
 'tyrion': {'arya', 'brienne'}, 
 'pod': {'jon'}, 
 'brienne': {'tyrion'}, 
 'arya': {'tyrion'}, 
 'jon': {'pod', 'jaime'}, 
 'jaime': {'pod', 'jon'}, 
 'ramsay': set()
}
    Note: you may assume that everyone listed in any of the friend sets also is included as a key in the dictionary. Also, do not worry about friends-of-friends-of-friends.

  4. instrumentedSelectionSort(a) and instrumentedBubbleSort(a) [10 pts] [autograded]
    Write the functions instrumentedSelectionSort(a) and instrumentedBubbleSort(a). Each of these should work just like the versions given in the course notes, except instead of returning None, they return a triple of values: the number of comparisons, the number of swaps, and the time in seconds to run the sort.

  5. selectionSortVersusBubbleSort() [10 pts] [manually graded]
    Write the function selectionSortVersusBubbleSort(). This function takes no parameters, and calls the instrumented functions you just wrote above, perhaps several times each, and then uses the results to empirically confirm that both selectionSort and bubbleSort are quadratic (O(n**2)), and then also prints a short but clear report making clear which sort runs in less time, which sort uses fewer comparisons, and which sort makes fewer swaps. This function returns nothing -- all the information is printed to the console.

  6. Bonus/Optional: threeWayMergesort [1 pt] [manually graded]
    First, write the function threeWayMergesort(L) that takes a list L and does a modified version of mergesort on L, where instead of combining two sorted sublists at a time, you should combine three sorted sublists at a time (so after one pass, you have sublists of size 3, and after two passes, sublists of size 9, and so on). You may not assume that the size of the list is a power of 3.

    Next, in a triple-quoted string just below your threeWayMergesort function, write a short proof that the function runs in O(nlogn) -- that is, in the same big-oh worst-case runtime as normal two-way mergesort. Then, write the function threeWayMergesortTiming() that empirically demonstrates that threeWayMergesort runs in the same big-oh as normal (two-way) mergesort (no more than a constant time faster or slower, even as n grows large). So all that extra work to write threeWayMergesort was for naught. Sigh. When you are done with this function, run it, get the timing data that proves your point, and include it with a very brief explanation at the end of that triple-quoted string just below threeWayMergesort.

  7. Bonus/Optional: keplerPolygons [up to 2.5 pts] [manually graded]
    Among his lesser-known exploits, the great German mathematician and astronomer Johannes Kepler studied how polygons can tile the plane or portions of the plane. Here you will write the function keplerPolygons() that takes no parameters and runs an animation that demonstrates one or more of these polygons (1 point for the first polygon, 0.5 point for each of the next 2):

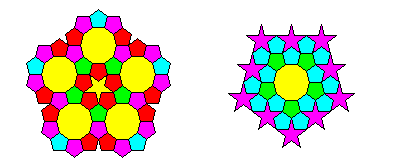
    For an additional half-point, bring at least one of these polygons to life so that they animate in an interesting way, such as rotating. And remember to use good style (no magic numbers!).
    Enjoy!!!