CMU 15-112 Fall 2018: Fundamentals of Programming and Computer Science
Homework 5 (Due Sunday 30-Sep, at 5pm)

• Reminder: all problems that are not explicitly marked COLLABORATIVE must be completed individually, as stated in the course syllabus.


• To start:
  1. Create a folder named 'week5'
  2. Download hw5.py to that folder.
  3. Edit hw5.py using Pyzo
  4. When you are ready, submit hw5.py to Autolab. For this hw, you may submit up to 6 times, but only your last submission counts.
• Do not use dictionaries or recursion this week.
• Do not hardcode the test cases in your solutions.


• IMPORTANT NOTE: Starting this week, we are not providing any test cases in the starter file. You should write your own test cases in the test functions to check your work!
  • Yes, Autolab is a great way to verify that your function is correct. But you only get 6 submissions on Autolab, so write and run your own tests first!

1. COLLABORATIVE Code-Writing: removeRowAndCol [20pts]
   Write removeRowAndCol first with a non-destructive approach, then with a destructive approach.
   
   Both functions take a list lst and two ints, row and col. They then both create a version of the list that has the given row and given column removed. You may assume that row and col are both legal values (that is, they are non-negative integers that are smaller than the largest row and column, respectively). For example, the list shown to the left would lead to the result shown on the right when called with the row 1 and the column 2.
   
   

   list	result
   [ [ 2, 3, 4, 5], [ 8, 7, 6, 5], [ 0, 1, 2, 3] ]	[ [ 2, 3, 5], [ 0, 1, 3] ]

   
   nondestructiveRemoveRowAndCol(lst, row, col): the non-destructive version should return a new list, and should not modify the provided list at all.
   
   destructiveRemoveRowAndCol(lst, row, col): the destructive version should modify the original list, and should not return anything (aka, None).
   
   Hint: writing test functions for non-destructive and destructive functions is a little different from writing ordinary test functions. Here is an example of a test case for a non-destructive function:
   
   
   # This is a test case for a non-destructive function. # The input list and output list lst = [ [ 2, 3, 4, 5], [ 8, 7, 6, 5], [ 0, 1, 2, 3] ] result = [ [ 2, 3, 5], [ 0, 1, 3] ] # Copy the input list so we can check it later import copy lstCopy = copy.deepcopy(lst) # The first assert is an ordinary test; the second is a non-destructive test assert(nondestructiveRemoveRowAndCol(lst, 1, 2) == result) assert(lst == lstCopy), "input list should not be changed"
   
   And here is an example of a test case for a destructive function:
   
   
   # This is a test case for a destructive function. # The input list and output list lst = [ [ 2, 3, 4, 5], [ 8, 7, 6, 5], [ 0, 1, 2, 3] ] result = [ [ 2, 3, 5], [ 0, 1, 3] ] # The first test is an ordinary test; the second is a destructive test assert(destructiveRemoveRowAndCol(lst, 1, 2) == None) assert(lst == result), "input list should be changed"


2. COLLABORATIVE Code-Revising: wordSearchWithWildcards(board, word) [10pts]
   Write wordSearchWithWildcards(board, word), which modifies our wordSearch algorithm from lecture so that it can include positive integers in the board, like so (see board[1][1]):
   
   
   board = [ [ 'p', 'i', 'g' ], [ 's', 2, 'c' ], [ 'r', 7, 'd' ] ] assert(wordSearchWithWildcards(board, "cows") == True)
   
   When matching a word, a positive integer on the board matches exactly that many letters in the word. So the board above contains the word "cow" starting from [1,2] heading left, since the 2 matches "ow". It also contains the word "cows" for the same reason. This board contains "pig" from [0,0], which uses no wildcards, as well as "be" from [1,1], which only uses wildcards! However, it does not contain "class" from [1,2], which would require three letters to match instead of two, or "road" from [2, 0], which would require two letters to match instead of seven.
   
   This function should return True if the board contains the word, and False otherwise. You are guaranteed that the first parameter will be a 2D rectangular list, and that the second parameter will be a string.
   
   You may use the wordSearch code from the course website or your lecture notes if you want, or you may re-write the algorithm from scratch. If you take the first approach, watch out: you'll need to modify the values that all three functions return, and you'll need to change the wordSearchFromCellInDirection function a great deal to account for possible wildcard numbers.


3. Code-Writing: Sudoku Logic [30pts]
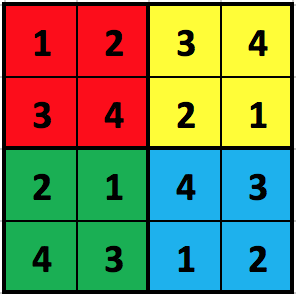
   This problem involves the game Sudoku, a game which is played on a 3²x3² grid, though we will generalize it to the N²xN² case, where N is a positive integer. First, read the top part (up to History) of the Wikipedia page on Sudoku so we can agree on the rules. For terminology, we will refer to each of the N² different N-by-N sub-regions as "blocks". The following figure shows each of the 4 blocks in a 2²x2² completed puzzle highlighted in a different color:
   
   
   
   While the next example shows the blocks of a 3²x3² incomplete puzzle:
   
   
   
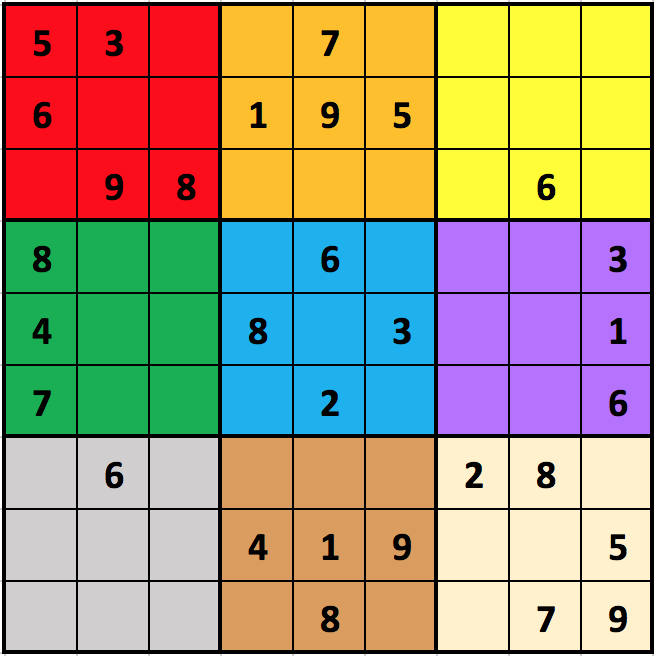
   For our purposes, we will number the blocks from 0 to N²-1 (hence, 0 to 8 in the figure), with block 0 in the top-left (red), moving across and then down (so, in the figure, block 1 is orange, block 2 is yellow, block 3 is green, block 4 is blue, block 5 is purple, block 6 is gray, block 7 is brown, and block 8 is tan). We will refer to the top row as row 0, the bottom row as row (N²-1), the left column as column 0, and the right column as column (N²-1).
   
   A Sudoku is in a legal state if all N⁴ cells are either blank (0) or contain a single integer from 1 to N² (inclusive), and if each integer from 1 to N² occurs at most once in each row, each column, and each block. A Sudoku is solved if it is in a legal state and contains no blanks.
   
   We will represent a Sudoku board as an N²xN² 2d list of integers, where 0 indicates that a given cell is blank. For example, here is how we would represent the 3²x3² Sudoku board in the figure above:
   
   

   [
     [ 5, 3, 0, 0, 7, 0, 0, 0, 0 ],
     [ 6, 0, 0, 1, 9, 5, 0, 0, 0 ],
     [ 0, 9, 8, 0, 0, 0, 0, 6, 0 ],
     [ 8, 0, 0, 0, 6, 0, 0, 0, 3 ],
     [ 4, 0, 0, 8, 0, 3, 0, 0, 1 ],
     [ 7, 0, 0, 0, 2, 0, 0, 0, 6 ],
     [ 0, 6, 0, 0, 0, 0, 2, 8, 0 ],
     [ 0, 0, 0, 4, 1, 9, 0, 0, 5 ],
     [ 0, 0, 0, 0, 8, 0, 0, 7, 9 ]
   ]
   

   
   With this description in mind, your task is to write some functions to indicate if a given Sudoku board is legal. To make this problem more approachable, we are providing a specific design for you to follow. And to make the problem more gradeable, we are requiring that you follow the design! You should solve the problem by writing the following functions in the order given:
   
   
   1. areLegalValues(values) [10pts]
      This function takes a 1d list of values, which you should verify is of length N² for some positive integer N and contains only integers in the range 0 to N² (inclusive). These values may be extracted from any given row, column, or block in a Sudoku board (and, in fact, that is exactly what the next few functions will do -- they will each call this helper function). The function returns True if the values are legal: that is, if every value is an integer between 0 and N², inclusive, and if each integer from 1 to N² occurs at most once in the given list (0 may be repeated, of course). Note that this function does not take a 2d Sudoku board, but only a 1d list of values that may or may not have been extracted from some Sudoku board. Also, note that this function must be non-destructive.
   
   
   2. isLegalRow(board, row) [5pts]
      This function takes a Sudoku board and a row number. The function returns True if the given row in the given board is legal (where row 0 is the top row and row (N²-1) is the bottom row), and False otherwise. To do this, your function must create a 1d list of length N² holding the values from the given row, and then provide these values to the areLegalValues function you previously wrote. (Actually, because areLegalValues is non-destructive, you do not have to copy the row; you may use an alias.)
   
   
   3. isLegalCol(board, col) [5pts]
      This function works just like the isLegalRow function, only for columns, where column 0 is the leftmost column and column (N²-1) is the rightmost column. Similarly to isLegalRow, this function must create a 1d list of length N² holding the values from the given column, and then provide these values to the areLegalValues function you previously wrote.
   
   
   4. isLegalBlock(board, block) [5pts]
      This function works just like the isLegalRow function, only for blocks, where block 0 is the left-top block, and block numbers proceed across and then down, as described earlier. Similarly to isLegalRow and isLegalCol, this function must create a 1d list of length N² holding the values from the given block, and then provide these values to the areLegalValues function you previously wrote. Note that getting the values from a block is much harder than getting the values from a row or col. You'll need to do a bit of math to find the starting row and col for each block based on the block's number.
   
   
   5. isLegalSudoku(board) [5pts]
      This function takes a Sudoku board (which you may assume is a N²xN² 2d list of integers), and returns True if the board is legal, as described above. To do this, your function must call isLegalRow over every row, isLegalCol over every column, and isLegalBlock over every block. See how helpful those helper functions are?


4. Sudoku Animation [40pts] [manually graded]
   Finally, you will write an animation that displays an interactive game allowing the user to play Sudoku. The Sudoku gameplay will be supported by the Sudoku logic you coded in the previous problem.
   
   For this animation, we will not require you to follow a specific appearance or a specific approach. You may build your Sudoku game any way you like, as long as it meets the following requirements:
   
   
   1. You must have a function called starterBoard() which returns the starter board for the game (defined as a 2D list of integers). You should then call starterBoard() in the init function to set up the initial board. You can then test the game by returning different boards in starterBoard. In fact, this is part of how we will test your code!
   
   
   2. The game must start by displaying the full N²xN² grid (in the format of a standard Sudoku board) and filling in the numbers already included in the starter board. Note that this doesn't need to be a 9x9 board- a 16x16 board should work too! (Note that it is OK for the game to break down if the starter board is too big to fit on the screen, like a 100x100 board. However, a 9x9 board should not be too big for the game).
   
   
   3. At all times, a single cell on the board is highlighted (using either a different color or different outline than the rest of the cells). The player can change the highlighted cell by clicking on a new cell, or by moving from the current cell with the up, down, left, and right arrows. Note that the game must support wraparound: typing up from row 0 leads to row N²-1, typing left from column 0 leads to column N²-1, typing down from row N²-1 leads to row 0, and typing right from column N²-1 leads to column 0. If the user clicks outside of the board, the highlighted cell should not change.
   
   
   4. To make a move, the player can press a single digit key to insert a number into an empty square. The move is only allowed if it will still result in a valid board, as determined by isLegalSudoku. The player can also clear the number from the highlighted square by pressing the backspace key.
   
   
   5. Initial numbers (squares that were filled in before game play began) should be a different color than numbers added by a player. In addition, the player cannot modify initial numbers.
   
   
   6. If, after a move, the player has properly filled in the entire board and won the game, a message should be displayed congratulating the player. After this, all further keypresses and mouse presses should be ignored.
   
   Note: there are many tiny details left unanswered here (how large should the board be? what colors should I use? exactly what should the board look like? should the blocks be outlined? what font for the numbers? etc, etc, etc). You have to decide them for yourself. Do not ask on piazza, do not ask at OH. Just decide. Keep it simple- we are not looking for anything amazing here, just a simple playable game that follows the rules above. Have fun!
   
   Addendum 1: If you want to test whether you can win the game properly, but don't want to play lots of Sudoku, consider testing with an almost-complete board such as this one:
   
   

   [
     [ 1, 2, 3, 4, 5, 6, 7, 8, 9],
     [ 5, 0, 8, 1, 3, 9, 6, 2, 4],
     [ 4, 9, 6, 8, 7, 2, 1, 5, 3],
     [ 9, 5, 2, 3, 8, 1, 4, 6, 7],
     [ 6, 4, 1, 2, 9, 7, 8, 3, 5],
     [ 3, 8, 7, 5, 6, 4, 0, 9, 1],
     [ 7, 1, 9, 6, 2, 3, 5, 4, 8],
     [ 8, 6, 4, 9, 1, 5, 3, 7, 2],
     [ 2, 3, 5, 7, 4, 8, 9, 1, 6]
   ]
   

   
   Addendum 2: You may solve this problem any way you wish. That said, here are some hints/suggestions for one approach to solving the problem. Use this or not as you wish. Good luck!
   Note: these videos are for a slightly older version of the problem, and may not be 100% accurate, but they're still a good guide.
   
   
   0. Read the problem
   1. Display the board
   2. Improve the board display
   3. Highlight a cell
   4. Show initial numbers
   5. Handle moves
   6. Win the game


5. Bonus/Optional: Sokoban Animation [3pts] [manually graded]
   First, read the Wikipedia page on Sokoban. Then, write the function playSokoban() that plays the game. Do not use any images. All drawing must be with graphics primitives (lines, rectangles, ovals, etc). Also, do not use any sound. Besides that, design as you will. The nicer the game, the more points awarded. Have fun!