CMU 15-112: Fundamentals of Programming and Computer Science
Class Notes: Efficiency

1. Big-O
2. Common Function Families
3. Efficiency
4. The Big Idea
5. Examples
   1. Sequences, Nesting, and Composition
      
   2. Python Builtins
      
   3. Searching
   4. Sorting
   5. sumOfSquares Examples
      

1. Big-O
   1. Describes behavior of a function as the size of its input grows
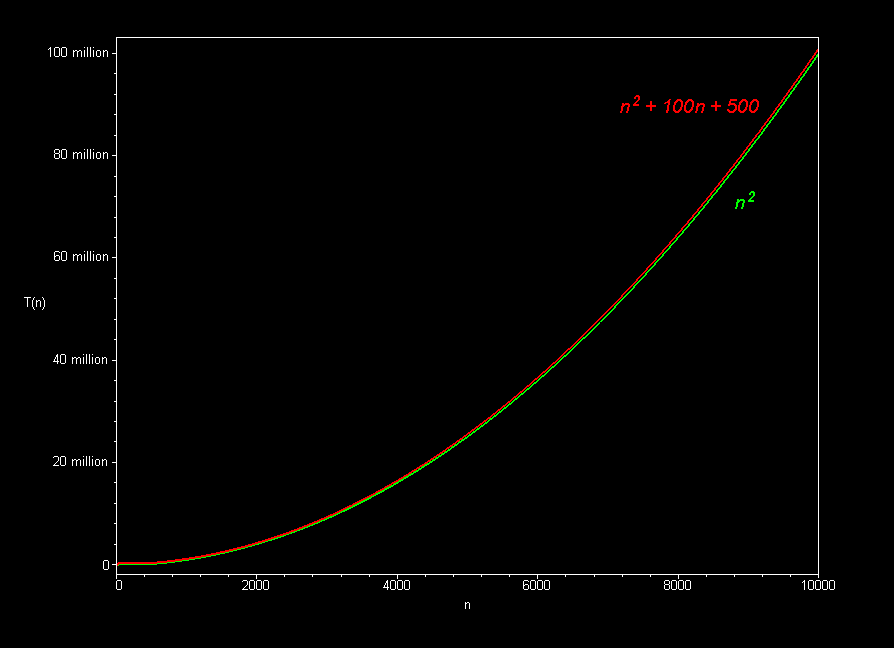
   2. Informally (for 15112): ignore all lower-order terms and constants
   3. Formally (after 15112): see here
   4. A few examples in math functions:
      • 3n² - 2n + 25 is O(n²)
      • 30000n² + 2n - 25 is O(n²)
      • 0.00000000001n² + 123456789n is O(n²)
      • 10nlog₁₇n + 25n - 17 is O(nlogn)


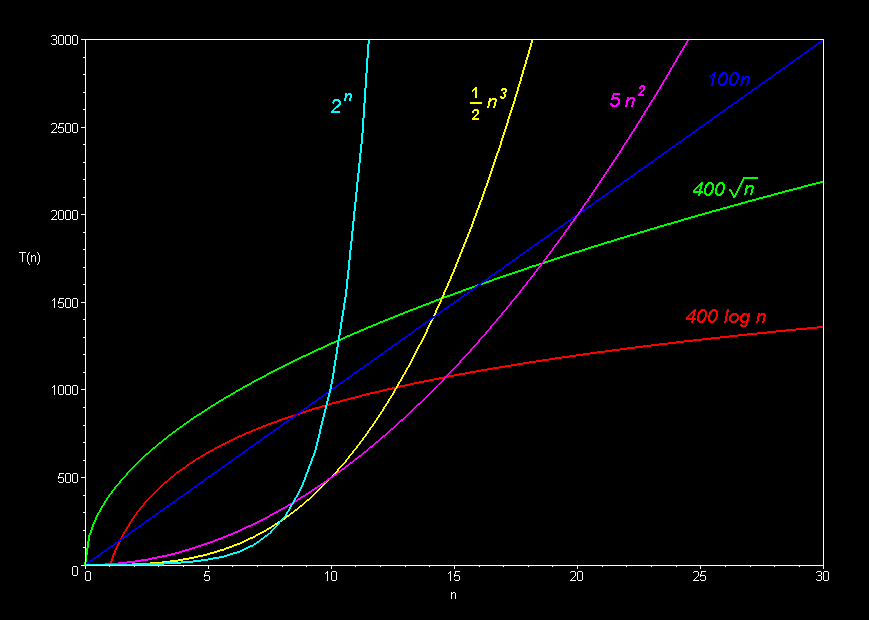
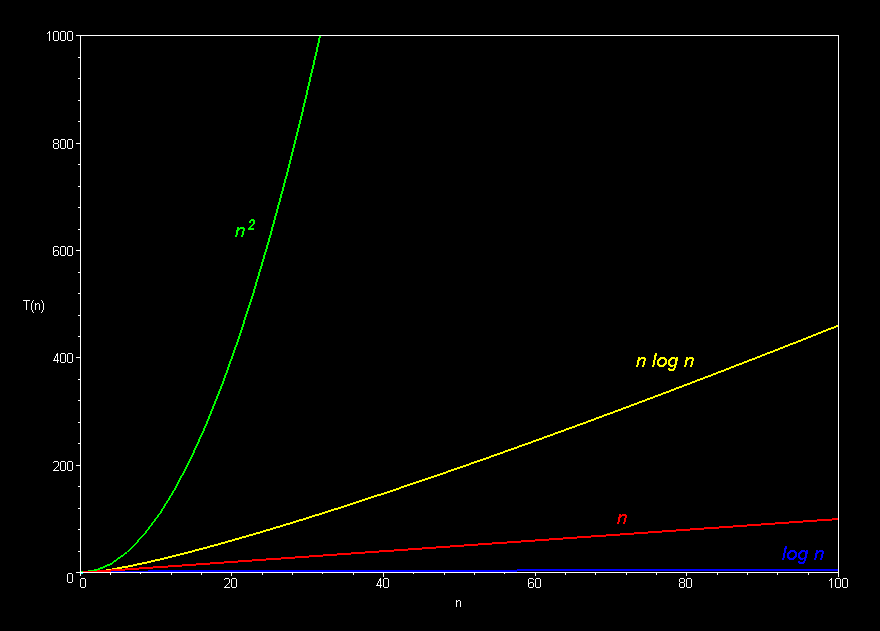
2. Common Function Families
   1. Constant O(1)
   2. Logarithmic O(logn)
   3. Square-Root O(n^0.5)
   4. Linear O(n)
   5. Linearithmic, Loglinear, or quasilinear O(nlogn)
   6. Quadratic O(n²)
   7. Exponential O(kⁿ)

Graphically (Images borrowed from here):







3. Efficiency
   When we say the program runs in O(N), we mean...
   • N is the size of our input
     • For a string s, N = len(s)
     • For a list lst, N = len(lst) (also true for sets, dictionaries, and other collections)
     • For an integer n, N = n
   • We can technically calculate Big-O for a number of program attributes, like time, space, bandwidth, etc. But in this class, we mainly care about time.
   • For time, we usually measure algorithmic steps rather than elapsed time (These share the same Big-O, but algorithmic steps are easier to precisely describe and reason over)
   • Algorithmic steps could be single lines of computation, or comparisons and swaps in a list, etc
   • Can verify by timing your code's execution with: time.time()
   • Note that you can measure worst-case or average case, or even other cases such as best case (which often is trivial to compute and not very useful in practice). For 15-112, we often omit this term (which is a notable simplification that you will not see in future courses), and we nearly always mean worst-case, which is quite useful and generally easier to compute than average-case.
   
   
4. The Big Idea
   • Each function family grows much faster than the one before it!
   • And: on modern computers, any function family is usually efficient enough on small n, so we only care about large n
   • So... Constants do not matter nearly as much as function families
   • Practically...
     • Do not prematurely or overly optimize your code
     • Instead: think algorithmically!!!


5. Examples
   1. Sequences, Nesting, and Composition
      • Sequencing
        
        # what is the total cost here? L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N L.sort() # This is O(NlogN) L.sort(reverse=True) # This is O(NlogN) L[0] -= 5 # This is O(1) print(L.count(L[0]) + sum(L)) # This is O(N) + O(N)
      
      
      • Nesting
        
        # what is the total cost here? L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N for c in L: # This loop's body is executed O(N) times L[0] += c # This is O(1) L.sort() # This is O(NlogN) print(L) # This is O(N) (why?)
      
      
      • Composition
        
        # what is the total cost here? def f(L): # assume L is an arbitrary list of length N L1 = sorted(L) # This is O(NlogN) return L1 # This is O(1) def g(L): # assume L is an arbitrary list of length N L1 = L * len(L) # This is O(N**2) (why?) return L1 # This is O(1) L = [ 52, 83, 78, 9, 12, 4 ] # assume L is an arbitrary list of length N L = f(g(L)) # What is the Big-O of this? print(L) # This is O(N**2) (why?)
   
   
   2. Python Builtins
      The efficiency of the built-in functions in Python will affect the efficiency of the functions they are used in. We do not expect you to memorize the builtin efficiencies; instead, you may look them up in the table provided below when needed. We will include the relevant subset of this table on quizzes and exams.
      
      

      General
      Function/Method	Complexity	Code Example
      Print	O(N)	# where N is the size of the input print(input)
      Range in Iteration	Number of iterations = (end - start)/step	for i in range(start, end, step):...
      Strings: s is a string with N characters
      Function/Method	Complexity	Code Example
      Len	O(1)	len(s)
      Membership	O(N)	"a" in s
      Get single character	O(1)	value = s[index]
      Get slice	O(end - start)	s[start:end]
      Get slice with step	O((end - start)/step)	s[start:end:step]
      Chr() and Ord()	O(1)	chr(s) ord(s)
      Concatentation	O(len(s1) + len(s2))	s3 = s1 + s2
      Character Type Methods	O(N)	s.isalnum() s.isalpha() s.isdigit() s.islower() s.isspace() s.isupper()
      String Edit Methods	O(N)	s.lower() s.upper() s.replace() s.strip()
      Substring Search Methods	O(N)	s.count() s.startswith() s.endswith() s.find() s.index()
      Lists: L is a list with N elements
      Function/Method	Complexity	Code Example
      Len	O(1)	len(L)
      Append	O(1)	L.append(value)
      Extend	O(K)	# len(a) = K L.extend(a)
      Concatentation with +=	O(K)	# len(a) = K L += a
      Concatentation with +	O(N + K)	# len(a) = K L = L + a
      Membership Check	O(N)	item in L
      Pop Last Value	O(1)	L.pop()
      Pop Intermediate Value	O(N)	L.pop(index)
      Count values in list	O(N)	L.count(item)
      Insert	O(N)	L.insert(index, value)
      Get value	O(1)	value = L[index]
      Set value	O(1)	L[index] = value
      Remove	O(N)	L.remove(value)
      Get slice	O(end - start)	L[start:end]
      Get slice with step	O((end - start)/step)	L[start:end:step]
      Sort	O(N log (N))	L.sort() sorted(L)
      Multiply	O(N*D)	#where D is an int A = L*D
      Minimum	O(N)	min(L)
      Maximum	O(N)	max(L)
      Copy	O(N)	copy.copy(L)
      Deep Copy	O(N*M)	# where L is a 2D list with N rows and M cols copy.deepcopy(L)
      Sets: s is a set with N elements
      Function/Method	Complexity	Code Example
      Len	O(1)	len(s)
      Membership	O(1)	elem in s
      Adding an Element	O(1)	s.add(elem)
      Removing an Element	O(1)	s.remove(elem) s.discard(elem)
      Union	O(len(s) + len(t))	s|t
      Intersection	O(min(len(s), len(t)))	s&t
      Difference	O(len(s))	s - t
      Clear	O(len(s))	s.clear()
      Copy	O(len(s))	s.copy()
      Dictionaries: d is a dictionary with N key-value pairs
      Function/Method	Complexity	Code Example
      Len	O(1)	len(d)
      Membership	O(1)	key in d
      Get Item	O(1)	value = d[key] d.get(key, defaultValue)
      Set Item	O(1)	d[key] = value
      Delete Item	O(1)	del d[key]
      Clear	O(N)	d.clear()
      Copy	O(N)	d.copy()

      
      For a more complete list, see here
   
   
   3. Searching
      • Linear search
        • Basic idea: check each element in turn
        • Use: find an element in an unsorted list
        • Cost: O(N)
      • Binary search
        • Basic idea: in a sorted list, check middle element, eliminate half on each pass
        • Uses:
          • Find an element in a sorted list
          • Number-guessing game (eg: guess a random number between 1 and 1000)
          • Find a root (zero) of a function with bisection (adapted binary search)
        • Cost: O(logN)
   
   
   4. Sorting
      1. Sorting Examples
         See here.
      
      
      2. Sorting Links
         
         • Wikipedia page on Sorting
         • David Eck's xSortLab applet (or you might try this jar file )
         • Excellent sorting animation website
         • Sorting algorithm animation video (15 algorithms in 6 minutes)
         • Even more sorting algorithm animations
      
      
      3. SelectionSort vs MergeSort
         • Definitions
           • Selection Sort: repeatedly select largest remaining element and swap it into sorted position
           • Mergesort: sort blocks of 1's into 2's, 2's into 4's, etc, on each pass merging sorted blocks into sorted larger blocks
         • Analysis
           This is mostly informal, and all you need to know for a 112-level analysis of these algorithms. You can easily find much more detailed and rigorous proofs on the web.
           • selectionsort
             On the first pass, we need N compares and swaps (N-1 compares and 1 swap).
             On the second pass, we need only N-1 (since one value is already sorted).
             On the third pass, only N-2.
             So, total steps are about 1 + 2 + ... + (N-1) + N = N(N+1)/2 = O(N²).
           
           
           • mergesort
             On each pass, we need about 3N compares and copies (N compares, N copies down, N copies back).
             So total cost = (3N steps per pass) x (# of passes)
             After pass 0, we have sorted lists of size 2⁰ (1)
             After pass 1, we have sorted lists of size 2¹ (2)
             After pass 2, we have sorted lists of size 2² (4)
             After pass k, we have sorted lists of size 2^k
             So we need k passes, where N = 2^k
             So # of passes = k = log₂N
             Recall that total cost = (3N steps per pass) x (# of passes)
             So total cost = (3N)(log₂N) = O(NlogN).
             Note: This is the theoretical best-possible Big-O for comparison-based sorting!
   
   
   5. sumOfSquares Examples
      Note: Run this code in Standard Python, as it will timeout if you run it in brython.
      # The following functions all solve the same problem: # Given a non-negative integer n, return True if n is the sum # of the squares of two non-negative integers, and False otherwise. def f1(n): for x in range(n+1): for y in range(n+1): if (x**2 + y**2 == n): return True return False def f2(n): for x in range(n+1): for y in range(x,n+1): if (x**2 + y**2 == n): return True return False def f3(n): xmax = int(n**0.5) for x in range(xmax+1): for y in range(x,n+1): if (x**2 + y**2 == n): return True return False def f4(n): xyMax = int(n**0.5) for x in range(xyMax+1): for y in range(x,xyMax+1): if (x**2 + y**2 == n): return True return False def f5(n): xyMax = int(n**0.5) for x in range(xyMax+1): y = int((n - x**2)**0.5) if (x**2 + y**2 == n): return True return False def testFunctionsMatch(maxToCheck): # first, verify that all 5 functions work the same print("Verifying that all functions work the same...") for n in range(maxToCheck): assert(f1(n) == f2(n) == f3(n) == f4(n) == f5(n)) print("All functions match up to n =", maxToCheck) testFunctionsMatch(100) # use larger number to be more confident import time def timeFnCall(f, n): # call f(n) and return time in ms # Actually, since one call may require less than 1 ms, # we'll keep calling until we get at least 1 secs, # then divide by # of calls we had to make calls = 0 start = end = time.time() while (end - start < 1): f(n) calls += 1 end = time.time() return float(end - start)/calls*1000 #(convert to ms) def timeFnCalls(n): print("***************") for f in [f1, f2, f3, f4, f5]: print ("%s(%d) takes %8.3f milliseconds" % (f.__name__, n, timeFnCall(f, n))) timeFnCalls(1001) # use larger number, say 3000, to get more accurate timing