CMU 15-112 Spring 2018: Fundamentals of Programming and Computer Science
Colab 5 (Due Thursday 15-Feb, at 10pm)

• This assignment is collaborative. That means you may work with other students enrolled in the course, and you may even help each other write code and debug. However, you must still type all of your own work, and you must fully understand the code that you submit. Even though this is collaborative, you may not directly copy any code from anyone, and you may not electronically share your code with anyone. See the syllabus for more details.
• List your collaboration partners (name and andrew id) in a comment on the first line of this file. If you collaborate with another student and do not include their name in a comment, it will be considered cheating. You may work alone if you want to, but we recommend working with others, as it generally leads to better learning.
• Be a good collaborator! Help everyone in your group, and accept their help if you need it. Don't be in a hurry to finish the problems. Instead, take your time and be sure that everyone in the group is following and understanding. The goal is to learn, not just to finish.
• If you're looking for more people to collaborate with, you can request to be paired up with other 112 students using this form.

---

• Starting this week, we will no longer be providing starter files or a linter for assignments. You are encouraged to make your own starter file using the format from previous weeks if you'd like. We will no longer run the linter on Autolab, but you should still follow all style rules and not use restricted tokens.

---



• To start:
  1. Go to your folder named 'week5'
  2. No starter code this week! You should build your own file (colab5.py) containing the functions below as well as proper testcases. You can use previous weeks' starter code as an example.
  3. Edit colab5.py using Pyzo
  4. When you are ready, submit colab5.py to Autolab. For this colab, you may submit up to 6 times, but only your last submission counts.
• Do not use dictionaries or recursion this week.
• Do not hardcode the test cases in your solutions.

1. isLegalSudoku(board) [75 pts]
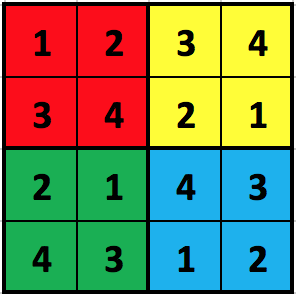
   This problem involves the game Sudoku, though we will generalize it to the N²xN² case, where N is a positive integer (and not just the 3²x3² case which is most commonly played). First, read the top part (up to History) of the Wikipedia page on Sudoku so we can agree on the rules. As for terminology, we will refer to each of the N² different N-by-N sub-regions as "blocks". The following figure shows each of the 4 blocks in a 2²x2² completed puzzle highlighted in a different color:
   
   
   While the next example shows the blocks of a 3²x3² incomplete puzzle:
   
   
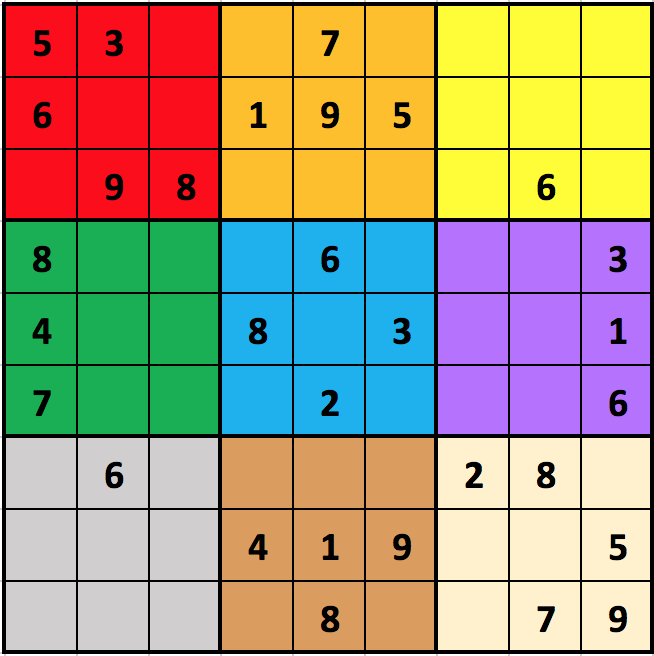
   For our purposes, we will number the blocks from 0 to N²-1 (hence, 0 to 8 in the figure), with block 0 in the top-left (red), moving across and then down (so, in the figure, block 1 is orange, block 2 is yellow, block 3 is green, block 4 is blue, block 5 is purple, block 6 is gray, block 7 is brown, and block 8 is tan). We will refer to the top row as row 0, the bottom row as row (N²-1), the left column as column 0, and the right column as column (N²-1).
   
   A Sudoku is in a legal state if all N⁴ cells are either blank (0) or contain a single integer from 1 to N² (inclusive), and if each integer from 1 to N² occurs at most once in each row, each column, and each block. A Sudoku is solved if it is in a legal state and contains no blanks.
   
   We will represent a Sudoku board as an N²xN² 2d list of integers, where 0 indicates that a given cell is blank. For example, here is how we would represent the 3²x3² Sudoku board in the figure above:

   [
     [ 5, 3, 0, 0, 7, 0, 0, 0, 0 ],
     [ 6, 0, 0, 1, 9, 5, 0, 0, 0 ],
     [ 0, 9, 8, 0, 0, 0, 0, 6, 0 ],
     [ 8, 0, 0, 0, 6, 0, 0, 0, 3 ],
     [ 4, 0, 0, 8, 0, 3, 0, 0, 1 ],
     [ 7, 0, 0, 0, 2, 0, 0, 0, 6 ],
     [ 0, 6, 0, 0, 0, 0, 2, 8, 0 ],
     [ 0, 0, 0, 4, 1, 9, 0, 0, 5 ],
     [ 0, 0, 0, 0, 8, 0, 0, 7, 9 ]
   ]
   

   With this description in mind, your task is to write some functions to indicate if a given Sudoku board is legal. To make this problem more approachable, we are providing a specific design for you to follow. And to make the problem more gradeable, we are requiring that you follow the design! So you should solve the problem by writing the following functions in the order given:
   
   
   1. areLegalValues(values) [15 pts]
      This function takes a 1d list of values, which you should verify is of length N² for some positive integer N and contains only integers in the range 0 to N² (inclusive). These values may be extracted from any given row, column, or block in a Sudoku board (and, in fact, that is exactly what the next few functions will do -- they will each call this helper function). The function returns True if the values are legal: that is, if every value is an integer between 0 and N², inclusive, and if each integer from 1 to N² occurs at most once in the given list (0 may be repeated, of course). Note that this function does not take a 2d Sudoku board, but only a 1d list of values that presumably have been extracted from some Sudoku board. Also, note that this function must be non-destructive.
   
   
   2. isLegalRow(board, row) [15 pts]
      This function takes a Sudoku board and a row number. The function returns True if the given row in the given board is legal (where row 0 is the top row and row (N²-1) is the bottom row), and False otherwise. To do this, your function must create a 1d list of length N² holding the values from the given row, and then provide these values to the areLegalValues function you previously wrote. (Actually, because areLegalValues is non-destructive, you do not have to copy the row; you may use an alias.)
   
   
   3. isLegalCol(board, col) [15 pts]
      This function works just like the isLegalRow function, only for columns, where column 0 is the leftmost column and column (N²-1) is the rightmost column. Similarly to isLegalRow, this function must create a 1d list of length N² holding the values from the given column, and then provide these values to the areLegalValues function you previously wrote.
   
   
   4. isLegalBlock(board, block) [15 pts]
      This function works just like the isLegalRow function, only for blocks, where block 0 is the left-top block, and block numbers proceed across and then down, as described earlier. Similarly to isLegalRow and isLegalCol, this function must create a 1d list of length N² holding the values from the given block, and then provide these values to the areLegalValues function you previously wrote.
   
   
   5. isLegalSudoku(board) [15 pts]
      This function takes a Sudoku board (which you may assume is a N²xN² 2d list of integers), and returns True if the board is legal, as described above. To do this, your function must call isLegalRow over every row, isLegalCol over every column, and isLegalBlock over every block. See how helpful those helper functions are?


2. isKingsTour(board) [25 pts]
   Background: in Chess, a King can move from any square to any adjacent square in any of the 8 possible directions. A King's Tour is a series of legal King moves so that every square is visited exactly once. We can represent a Kings Tour in a 2D list where the numbers represent the order the squares are visited, going from 1 to N². For example, consider these 2D lists:

      [ [  3, 2, 1 ],        [ [  1, 2, 3 ],      [ [ 3, 2, 1 ],
        [  6, 4, 9 ],          [  7, 4, 8 ],        [ 6, 4, 0 ],
        [  5, 7, 8 ] ]         [  6, 5, 9 ] ]       [ 5, 7, 8 ] ]
   

   The first is a legal Kings Tour but the second is not, because there is no way to legally move from the 7 to the 8, and the third is not, because it contains a 0 which is out of range. Also, this should work not just for 3x3 boards but for any NxN board. For example, here is a legal Kings Tour in a 4x4 board:

       [ [  1, 14, 15, 16],
         [ 13,  2,  7,  6],
         [ 12,  8,  3,  5],
         [ 11, 10,  9,  4]
       ]
   

   With this in mind, write the function isKingsTour(board) that takes a 2D list of integers, which you may assume is NxN for some N>0, and returns True if it represents a legal Kings Tour and False otherwise.