CMU 15-112 Spring 2018: Fundamentals of Programming and Computer Science
Homework 10 (Due Sunday 1-Apr, at 8pm)

• This assignment is SOLO. This means you may not look at other student's code or let other students look at your code for these problems. See the syllabus for details.
• Important Note: the autograder we use breaks when it tries to import tkinter. Therefore, all of your tkinter code must be included after a comment that reads #ignore_rest. The autograder will only grade code that appears before #ignore_rest. This means that your solutions to flatten and solveABC must appear before #ignore_rest, and runTeddyFractalViewer must appear after.
• The autograder also fails to work properly if any errors (including assertion errors) occur when the file is run. Putting all of your test code underneath ignore_rest is a good way to make sure your code can be autograded properly!

---

• To start:
  1. Go to your folder named 'week10'
  2. Create a file named hw10.py in that folder
  3. Edit hw10.py using Pyzo
  4. When you're done, submit hw10.py to Autolab. You may submit up to 5 times.
• Do not hardcode the test cases in your solutions.

1. Lab Problems [10 pts]
   Attend your scheduled lab on Friday. While there, complete the basic problem and make a real attempt at the advanced problem. One of the TAs will record your participation by hand.


2. flatten(lst) [25 pts]
   Write the recursive and non-destructive function flatten(lst), which takes a list which may contain lists (which themselves may contain lists, and so on), and returns a single list (which does not contain any other lists) which contains each of the non-lists, in order, from the original list. This is called flattening the list. For example:

   flatten([1,[2]]) returns [1,2]
   flatten([1,2,[3,[4,5],6],7]) returns [1,2,3,4,5,6,7]
   flatten(['wow', [2,[[]]], [True]]) returns ['wow', 2, True]
   flatten([]) returns []
   flatten([[]]) returns []
   



3. runTeddyFractalViewer() [30 pts]
   Below the #ignore_rest line, write a function teddyFace(canvas, xc, yc, r) that draws a circular-shaped face of a teddy bear, without ears. This function takes as input a canvas to draw on, the (xc, yc) coordinates of the center of the face, and the radius r of the face. While you need not be pixel-perfect, try to make the face reasonably similar to the one in the image below.
   
   Hint: to draw the mouth, you should use the function create_arc(...) of Tkinter with the optional parameters style and extent. For more information about this function read the documentation here.
   
   Also below the #ignore_rest line, and exploiting your previous function teddyFace, write a function fractalTeddy(canvas, xc, yc, r, level) that recursively draws a character with the face you previously defined, and a recursively downsized version of that same face as ears. Your function will take as parameter a canvas to draw on, the (xc, yc) coordinates of the center of the face, the radius r of the face, and an integer level representing the maximum depth of recursion. The radius of each ear is exactly half the radius of the face. The following figure shows an example of a Fractal Teddy with maximum recursion level (depth) of 6.
   
   
   
   Also below the #ignore_rest line, write the function runTeddyFractalViewer() that behaves similarly to the Sierpinsky Triangle example in the course notes, where pressing arrows changes the depth of the recursion (though of course here you'll display recursive Teddy Bears and not Sierpinsky Triangles).


4. solveABC(constraints, aLocation) [35 pts]
   This problem is inspired by the "ABC Path" problems at BrainBashers.com. For more (optional) info, check this out. In what we will call an "ABC Puzzle", you are given a 5x5 board like this:
   
   
   
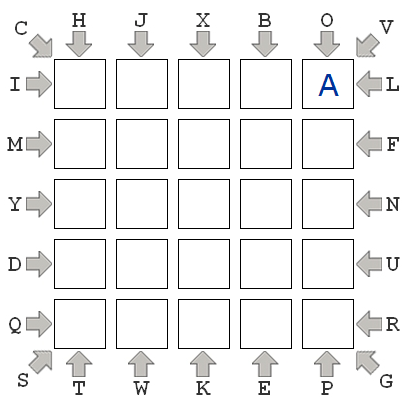
   It is an empty board except that it contains a single "A" in an arbitrary cell. Also, the letters from "B" to "Y" are arranged around the outside of the board in an arbitrary order, along with arrows that constrain those letters to a certain row, column, or diagonal. For example, in the image, we see the "H" and "T" are constrained to column 0, "L" and "I" are constrained to row 0, and "C" and "G" are constrained to the column running from (0,0) to (4,4). The goal of this puzzle is to place every letter from "B" to "Y" on the board such that: (1) each letter from "B" to "Y" is placed in the row, column, or diagonal in which it is constrained; and (2) each letter from "B" to "Y" is placed adjacent (including diagonally) to the previous letter (so "B" is adjacent to "A", and "C" is adjacent to "B", and so on).
   
   A solution to the puzzle shown above is:
   
   
   
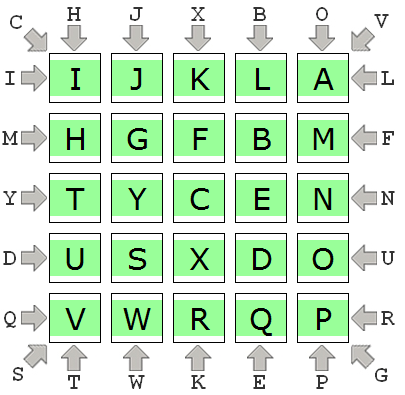
   Be sure you understand why this solves the puzzle! If you are unsure, go to the link at BrainBashers.com and read more about this kind of puzzle, including this help page, and maybe try to solve a few more of them (the puzzles include a button you can press to get the solutions!).
   
   Now, for us to represent one of these puzzles in Python, we have to represent the constraints. We'll do that using a dictionary. The dictionary will have three keys: "rows", "cols", and "diags". "rows" and "cols" will each map to another dictionary which maps indexes of rows/cols to lists of the letters constrained to that row/col. "diags" will map to another dictionary that has two keys, "left" and "right", which map to the letters constrained to the left-down and right-down diagonals. Thus, in the given example, the constraints are:
   
   
   constraints = { "rows" : { 0 : ["I", "L"], 1 : ["M", "F"], 2 : ["Y", "N"], 3 : ["D", "U"], 4 : ["Q", "R"] }, "cols" : { 0 : ["H", "T"], 1 : ["J", "W"], 2 : ["X", "K"], 3 : ["B", "E"], 4 : ["O", "P"] }, "diags" : { "left" : ["C", "G"], "right" : ["V", "S"] } }
   
   We also need to specify the position of the "A", which we will do as a (row,col) tuple, as such:
   
   aLocation = (0,4)
   
   With this in mind, write the function solveABC(constraints, aLocation), that takes constraints and the location of the "A", which together define an ABC Puzzle, and returns a completed board which solves the puzzle, or None if no such board exists. Here is a test function that is based on the puzzle used in the example above (notice how the constraints and aLocation match the unsolved puzzle, and the resulting board matches the solved puzzle):
   
   
   def testSolveABC(): print('Testing solveABC()...', end='') constraints = { "rows" : { 0 : ["I", "L"], 1 : ["M", "F"], 2 : ["Y", "N"], 3 : ["D", "U"], 4 : ["Q", "R"] }, "cols" : { 0 : ["H", "T"], 1 : ["J", "W"], 2 : ["X", "K"], 3 : ["B", "E"], 4 : ["O", "P"] }, "diags" : { "left" : ["C", "G"], "right" : ["V", "S"] } } aLocation = (0,4) board = solveABC(constraints, aLocation) solution = [ ['I', 'J', 'K', 'L', 'A'], ['H', 'G', 'F', 'B', 'M'], ['T', 'Y', 'C', 'E', 'N'], ['U', 'S', 'X', 'D', 'O'], ['V', 'W', 'R', 'Q', 'P'] ] assert(board == solution) print('Passed!')
   
   Notes/Hints:
   • To receive any credit for this problem, you must solve it recursively, even if you could dream up a non-recursive solution!
   • This is a backtracking problem. Study the backtracking template and backtracking examples; they will help.
   • You will want to make judicious use of a wrapper function or optional parameters.
   • Your solution to flatten might come in handy here...


5. Bonus: Rectangula [3 pts]
   In the game Rectangula, the goal of the player is to place numbers in boxes in order to fill the grid with rectangles. Watch here for a demonstration:
   
   Your task is to write the function solveRectangula(board). This function takes a board which is a 2d list of integers corresponding to the board you see in the video, where blank cells contain 0's. Your function should return a solution to that board, which consists of a list of rectangles (in any order) such that:
   
   1. Every rectangle in your solution is on the board.
   2. No two rectangles in your solution overlap.
   3. Every non-zero number on the board is inside exactly one rectangle in your solution, and the area of that rectangle matches the number.
   4. And every rectangle in your solution contains exactly one number on the board.
   
   Note that your rectangles must be of the form (row0, col0, width, height), where (row0, col0) marks the top-left of the rectangle (remember, rows increase vertically, cols increase horizontally), and width is the total number of columns, and height is the total number of rows (so width*height is the area of the rectangle).
   
   If there is no possible solution, your function should return None.
   
   To test your function, download and use the file hw10_rectangula_tester.py. You should place that code in the same folder as your hw10.py file. Do not include any code from the tester file in your hw10.py file! Instead, include these lines in your hw10.py file, below the #ignore_rest line:
   
   
   ############################################### # ignore_rest ############################################### # Place these imports in hw10.py below the ignore_rest line! from hw10_rectangula_tester import testSolveRectangula from hw10_rectangula_tester import playRectangula testSolveRectangula(solveRectangula) playRectangula(solveRectangula)
   
   Then, when you run your hw10.py file, you'll run the testSolveRectangula function and the playRectangula function in rectangula-tester.py. Have fun!